Defining a core microbiome

Author

Fiama Guevara

Published

March 15, 2024


Introduction: The core microbiome

Let’s start understanding what is considered a core microbiome. It comprises the members shared among two or more microbial assemblages associated with a habitat. To define a core microbiome we can consider parameters such as composition (taxonomic membership or community function), phylogeny, persistence, connectivity (biotic/abiotic interactions).

Why is important to define a core microbiome? Important to know the role of key microorganisms and their functions within and across ecosystems. Commonly occurring microorganisms are likely critical to the function of that community. Also, it helps us to define what is a ‘healthy’ community and predict its responses to perturbation.

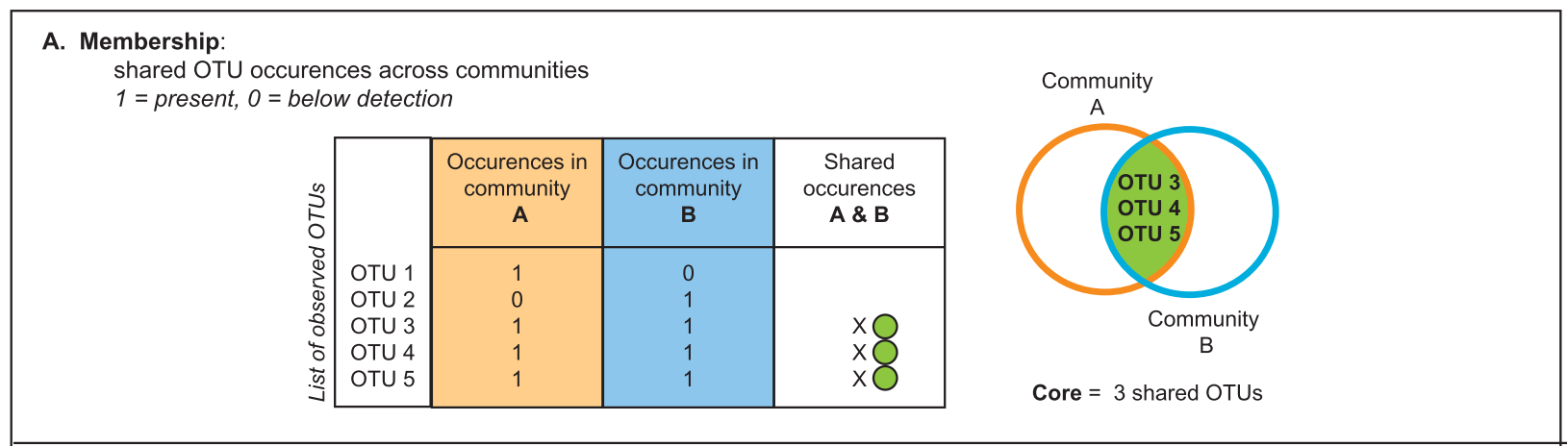
There are several approaches to define a core microbiome1:

1. Membership (taxonomically defined shared taxa)

Based on presence/absence of taxa. The Sørenson’s index could be applied to determine a membership-based core microbiome since it accounts for the number of shared and unique OTUs/ASVs per group. Membership-based core microbiome definition depends on sequencing efforts. Sequencing depth could change proportions.

Figure from Shade et al. 2012

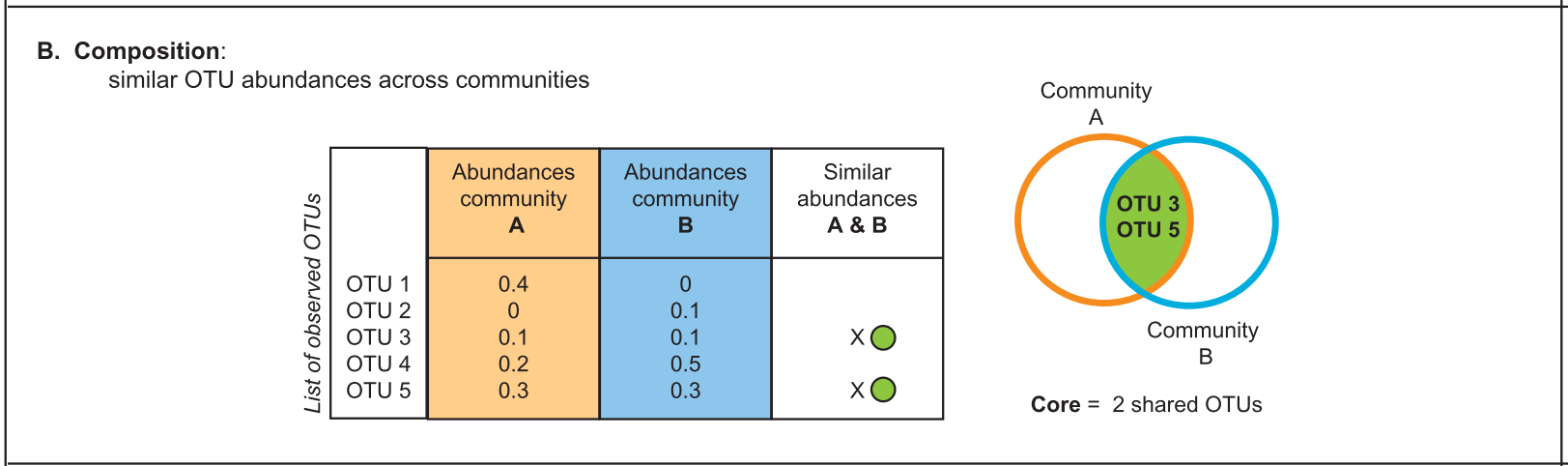
2. Composition (relative abundance)

Accounts for the representation in the community using relative abundance of each OTU/ASV. Dominant and rare members can contribute in different ways to the community. You might focus your analysis in a specific group.

Figure from Shade et al. 2012

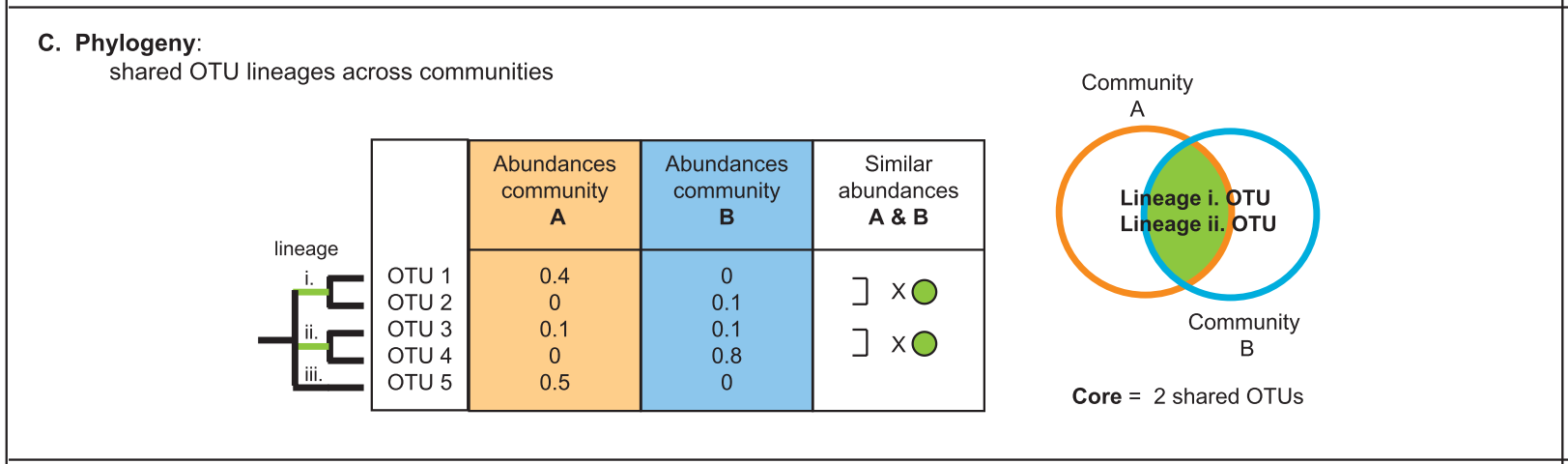
3. Phylogenetic and functional redundancy

Phylogenetic redundancy refers to multiple members from the same lineage present in a microbiome, whereas functional redundancy to members within a microbiome are performing the same functions (e.g. nitrogen fixation). Functional redundancy can help the microbiome buffer disturbance responses.

Figure from Shade et al. 2012

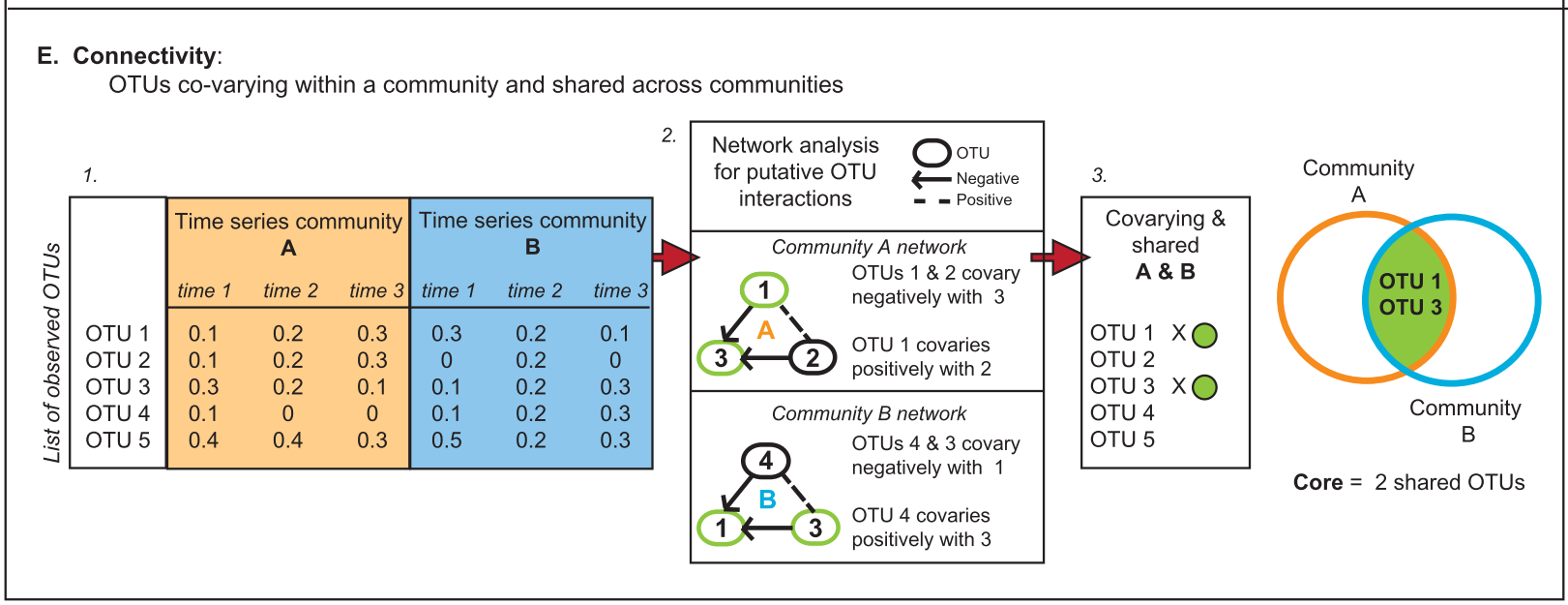
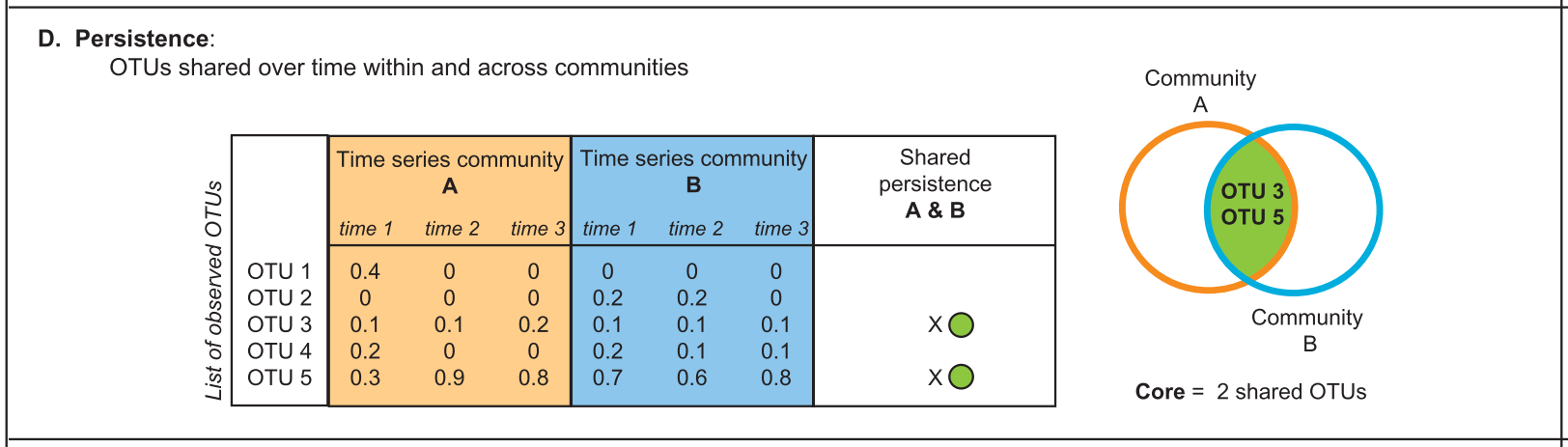
4. Persistence (temporal and spatial)

Persistence/transience concepts are similar to dominance/rarity. For example: when determining plant-associated microbiomes present across developmental stages.

Figure from Shade et al. 2012

5. Connectivity (co-variation within and shared communities)

Networks analyses can generate hypotheses about interacting members. We can assess the number or strength of interactions within a microbial community. This information could be more informative for predicting and managing core microbiomes across systems.

Figure from Shade et al. 2012


1 Setting up

If you need to start a new RStudio Server session at OSC or open your RStudio Project, see the box below.

Start an RStudio Server job

  1. Log in to OSC at https://ondemand.osc.edu.
  2. Click on Interactive Apps (top bar) and then RStudio Server (all the way at the bottom).
  3. Fill out the form as follows:
    • Cluster: Pitzer
    • R version: 4.3.0
    • Project: PAS2714
    • Number of hours: 4
    • Node type: any
    • Number of cores: 4
  4. Click Launch and once your job has started, click Connect to RStudio Server.

Open your RStudio Project

  • Your RStudio Project at /fs/ess/PAS2714/users/<user> may have automatically opened. You can see whether a Project is open, and if so, which one, in the top-right of your screen (left screenshot below)
  • If your Project isn’t open, click on the R-in-a-box icon to open it (right screenshot below):

Here, the project jelmer is open.
Your Project name is also your username.

Opening an RStudio Project

Create a new script (Optional)

Click File > New file > R script, and immediately save the new file (File > Save as) as core.R inside your scripts directory2.

We recommend that you copy-and-paste (or type, if you prefer) code from this webpage into your script and then execute the code. That way, you’ll have a nice record of what you did, exactly.

Load packages

# Set the R library to load packages from
.libPaths("/fs/ess/PAS0471/jelmer/R/metabar")
dyn.load("/fs/ess/PAS0471/jelmer/software/GLPK/lib/libglpk.so.40", local = FALSE)
# Load the packages
library(tidyverse)
library(microbiome)
library(phyloseq)
library(ggvenn)

Load the phyloseq object

Read the phyloseq object containing your data:

ps.dataset <- readRDS("results/ps_fulldata/bac22rot_w_ASV.rds")

Take a look of your metadata and the variables you want to analyse. We will focus on Rotation.

sample_data(ps.dataset)
           Year Location Rotation  Plot TRT Block Sampling.Date
T22NW102AB 2022    NWARS       CS 102AB   2   100    June, 2022
T22NW102C  2022    NWARS       CS  102C   7   100    June, 2022
T22NW103AB 2022    NWARS      CSW 103AB   3   100    June, 2022
T22NW103C  2022    NWARS      CSW  103C   8   100    June, 2022
T22NW201AB 2022    NWARS      CSW 201AB   3   200    June, 2022
T22NW201C  2022    NWARS      CSW  201C   8   200    June, 2022
T22NW203A  2022    NWARS       CS  203A   7   200    June, 2022
T22NW203BC 2022    NWARS       CS 203BC   2   200    June, 2022
T22NW305AB 2022    NWARS       CS 305AB   2   300    June, 2022
T22NW305C  2022    NWARS       CS  305C   7   300    June, 2022
T22NW403A  2022    NWARS       CS  403A   7   400    June, 2022
T22NW403BC 2022    NWARS       CS 403BC   2   400    June, 2022
T22NW404A  2022    NWARS      CSW  404A   8   400    June, 2022
T22NW404BC 2022    NWARS      CSW 404BC   3   400    June, 2022
T22W101AB  2022     WARS       CS 101AB   2   100    June, 2022
T22W101C   2022     WARS       CS  101C   7   100    June, 2022
T22W103AB  2022     WARS      CSW 103AB   3   100    June, 2022
T22W103C   2022     WARS      CSW  103C   8   100    June, 2022
T22W204A   2022     WARS      CSW  204A   8   200    June, 2022
T22W204BC  2022     WARS      CSW 204BC   3   200    June, 2022
T22W205A   2022     WARS       CS  205A   7   200    June, 2022
T22W205BC  2022     WARS       CS 205BC   2   200    June, 2022
T22W303AB  2022     WARS      CSW 303AB   3   300    June, 2022
T22W303C   2022     WARS      CSW  303C   8   300    June, 2022
T22W304AB  2022     WARS       CS 304AB   2   300    June, 2022
T22W304C   2022     WARS       CS  304C   7   300    June, 2022
T22W403AB  2022     WARS       CS 403AB   2   400    June, 2022
T22W403C   2022     WARS       CS  403C   7   400    June, 2022
T22W404A   2022     WARS      CSW  404A   8   400    June, 2022
T22W404BC  2022     WARS      CSW 404BC   3   400    June, 2022


2 Approach 1: Composition (relative abundance)

  1. Transform the ASV count table to compositional data (relative abundance). For that we will use the R package microbiome (previously installed) with the function transform.
ps.dataset.cm <- microbiome::transform(ps.dataset, "compositional")
  1. Determine the core taxa by the variable of interest (Rotation).For this you will subset the data by Rotation variable.
ps.CS <- subset_samples(ps.dataset.cm, Rotation == "CS")
ps.CSW <- subset_samples(ps.dataset.cm, Rotation == "CSW")

Then, get the core taxa using the function core_members from the R package microbiome.

core.taxa.CS <- core_members(ps.CS, detection = 0.001, prevalence = 95/100)
core.taxa.CSW <- core_members(ps.CSW, detection = 0.001, prevalence = 95/100)
How to set detection and prevalence threasholds

Detection (limit of detection) will be the minimum relative abundance value at which taxa will be selected. This can be set by the user or determined empirically based on sequencing depth.

Prevalence is the proportion of samples that will be selected given a detection threshold.

Example (click here)

Consider this mock data for relative abundance of Pseudomonas fluorescens in 10 soil microbiome samples:

Sample Relative abundance (%)
1 0.002
3 0.49
4 7.8
5 12.1
6 0.52
7 0.2
8 0.06
9 9.1
10 0.08

Based on detection values, the prevalence will change. Lower detection threshold equals higher prevalence:

Detection Prevalence
1 3/10
0.1 6/10
0.01 9/10
  1. Create a list with the selected core taxa for both subsets.
cores.list <- list(CS = core.taxa.CS, CSW = core.taxa.CSW)
cores.list #To see the list of core taxa (ASVs) by Rotation
$CS
 [1] "ASV_1372" "ASV_1425" "ASV_1426" "ASV_1723" "ASV_1737" "ASV_2316"
 [7] "ASV_2440" "ASV_2450" "ASV_2483" "ASV_2545" "ASV_2605" "ASV_2635"
[13] "ASV_2825" "ASV_3076" "ASV_3576" "ASV_3587" "ASV_3592" "ASV_3986"
[19] "ASV_4073" "ASV_4082" "ASV_4242" "ASV_4348" "ASV_4391" "ASV_4478"
[25] "ASV_4504" "ASV_4555" "ASV_4565" "ASV_4642" "ASV_5779" "ASV_5791"
[31] "ASV_6609" "ASV_7160" "ASV_7731" "ASV_7736" "ASV_7822" "ASV_7847"
[37] "ASV_7848" "ASV_8079"

$CSW
 [1] "ASV_1367" "ASV_1372" "ASV_1388" "ASV_1425" "ASV_1426" "ASV_1723"
 [7] "ASV_1737" "ASV_1863" "ASV_2316" "ASV_2440" "ASV_2450" "ASV_2483"
[13] "ASV_2545" "ASV_2605" "ASV_2619" "ASV_2635" "ASV_2825" "ASV_2896"
[19] "ASV_3076" "ASV_3576" "ASV_3592" "ASV_3898" "ASV_3962" "ASV_3986"
[25] "ASV_4059" "ASV_4073" "ASV_4082" "ASV_4242" "ASV_4391" "ASV_4477"
[31] "ASV_4478" "ASV_4504" "ASV_4521" "ASV_4565" "ASV_4642" "ASV_4654"
[37] "ASV_4655" "ASV_5760" "ASV_5791" "ASV_6609" "ASV_6960" "ASV_7160"
[43] "ASV_7349" "ASV_7731" "ASV_7736" "ASV_7822" "ASV_7848" "ASV_7858"
[49] "ASV_8079"
  1. Get the list of shared taxa from the taxa table of your dataset.
tax.table.ps <- as.data.frame(tax_table(ps.dataset))

shared.taxa <-  core.taxa.CS[core.taxa.CS %in% core.taxa.CSW]
tax <- tax.table.ps[which(row.names(tax.table.ps) %in% shared.taxa ),]
  1. Get the list of unique taxa in Rotation CS.
unique.taxa.CS <-  core.taxa.CS[!core.taxa.CS %in% core.taxa.CSW]
tax.CS <- tax.table.ps[which(row.names(tax.table.ps) %in% unique.taxa.CS),]
  1. Get the list of unique taxa in Rotation CSW.
unique.taxa.CSW <-  core.taxa.CSW[!core.taxa.CSW %in% core.taxa.CS]
tax.CSW <- tax.table.ps[which(row.names(tax.table.ps) %in% unique.taxa.CSW),]
  1. Plot a Venn Diagram.
plot <- ggvenn(cores.list, fill_color = c("#0073C2FF", "#EFC000FF"),
            stroke_size = 0.5, set_name_size = 5, text_size = 5,
            show_percentage = T)
print(plot)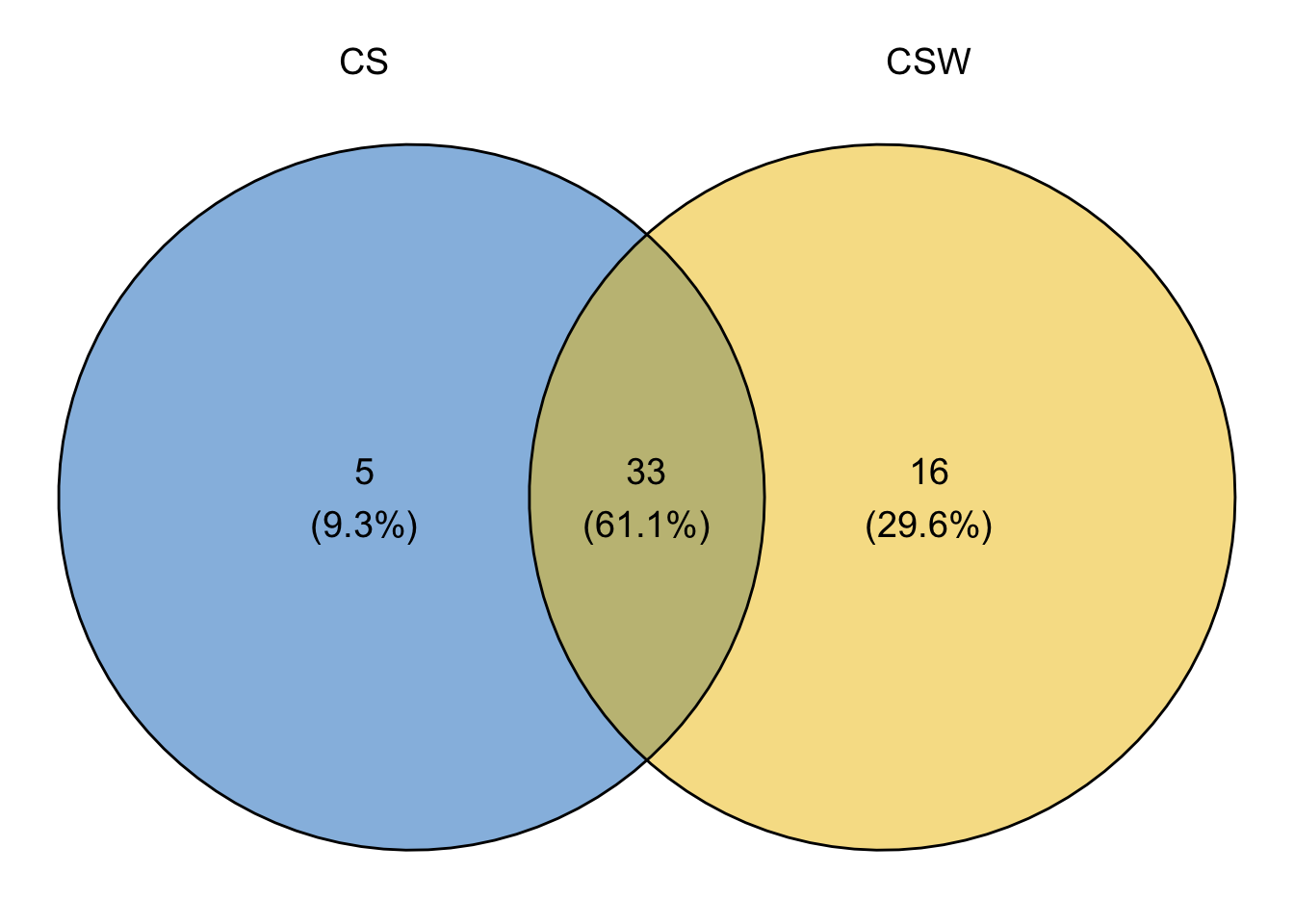


3 Approach 2: Membership and Composition

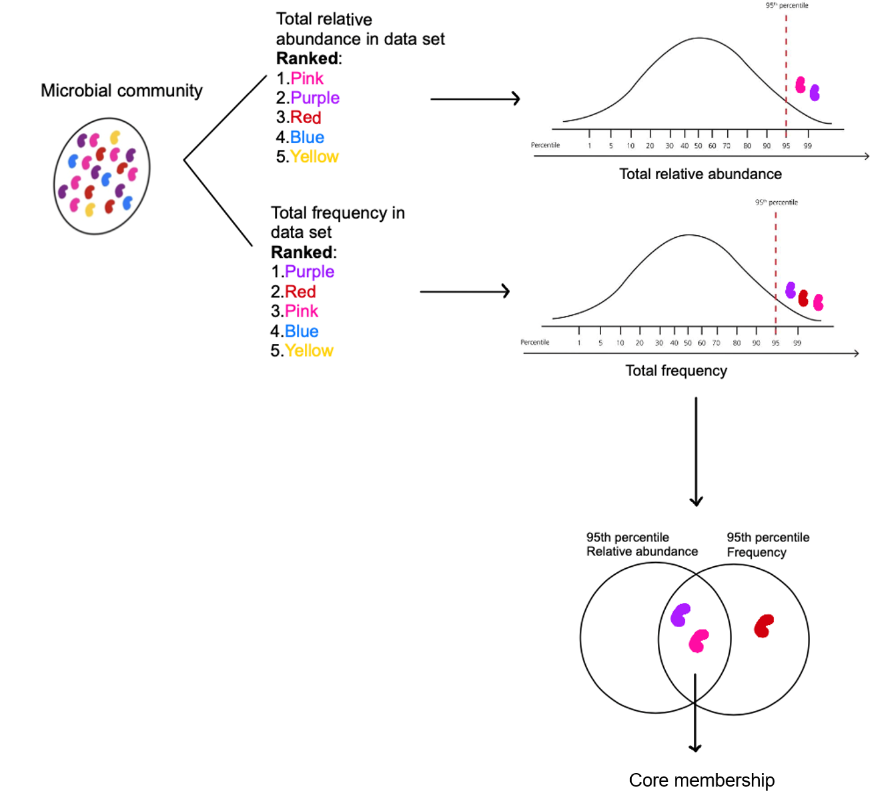
This approach takes into account presence/absence and relative abundance to select shared taxa. The threshold could arbitrary be set but here we will follow the 95th percentile approach3. That means that we will assign core membership to taxa that fell within the 95th percentile of the ranked frequency and ranked relative abundance within the whole data.

Diagram of how the 95th percentile frequency and abundance core taxa were identified. The distribution of total relative abundance and frequency of taxa is assessed and the those ranked within the 95th percentile (top 5%) are selected as core. Figure from Cantoran et al. 2023.

  1. Create a data frame from the phyloseq object.
df <- psmelt(ps.dataset.cm)
  1. Take the total Relative Abundance sum of each genus.
df.RA <- aggregate(df$Abundance, by = list(Genus = df$Genus), FUN=sum) 
df.RA <- dplyr::rename(df.RA, TotalRA = `x`)
  1. Determining 95th quantile of the RA data.
quantile.95.abund <- quantile(df.RA$TotalRA, 0.95)
  1. Selecting for genera that fit the 95th cutoff.
taxa.95 <- subset(df.RA, TotalRA >= quantile.95.abund) 
taxa.95.genus <- taxa.95$Genus
  1. Determine the frequency 95th cutoff. We go back and use the original phyloseq object and agglomerate the data by Genus tax rank (it could be any tax rank you want e.g., Phylum, Family).
ps.genus <- tax_glom(ps.dataset, "Genus")
ASVs.genus <- otu_table(ps.genus)
df.ASVs.genus <- as.data.frame(ASVs.genus)
rownames(df.ASVs.genus) <- as.data.frame(tax_table(ps.genus))$Genus
  1. Create a table of presence/abundance of ASVs. We will use 1 if present, 0 if not.
df.PA <- 1*((df.ASVs.genus>0)==1)
Occupancy <- rowSums(df.PA)/ncol(df.PA) #Calculate occupancy
df.Freq <- as.data.frame(cbind(df.PA, Occupancy))
df.Freq <- tibble::rownames_to_column(df.Freq, "Genus")
  1. Determining 95th quantile of the presence/abundance table.
quantile.95.freq <- quantile(df.Freq$Occupancy, 0.95)
  1. Select the genera that fit the 95th cutoff.
Freq.95 <- subset(df.Freq, Occupancy >= quantile.95.freq) #select cutoff 
Freq.95.genus <- Freq.95$Genus

Quantile.95 <- merge.data.frame(Freq.95, taxa.95, by = "Genus")

Use the Freq.95.genus and taxa.95.genus data:

Core.95.list <- list(Frequency = Freq.95.genus, Relative_abundance = taxa.95.genus)

plot.VennD <- ggvenn(Core.95.list,
            stroke_size = 0.5, set_name_size = 3.2, text_size = 3)

print(plot.VennD)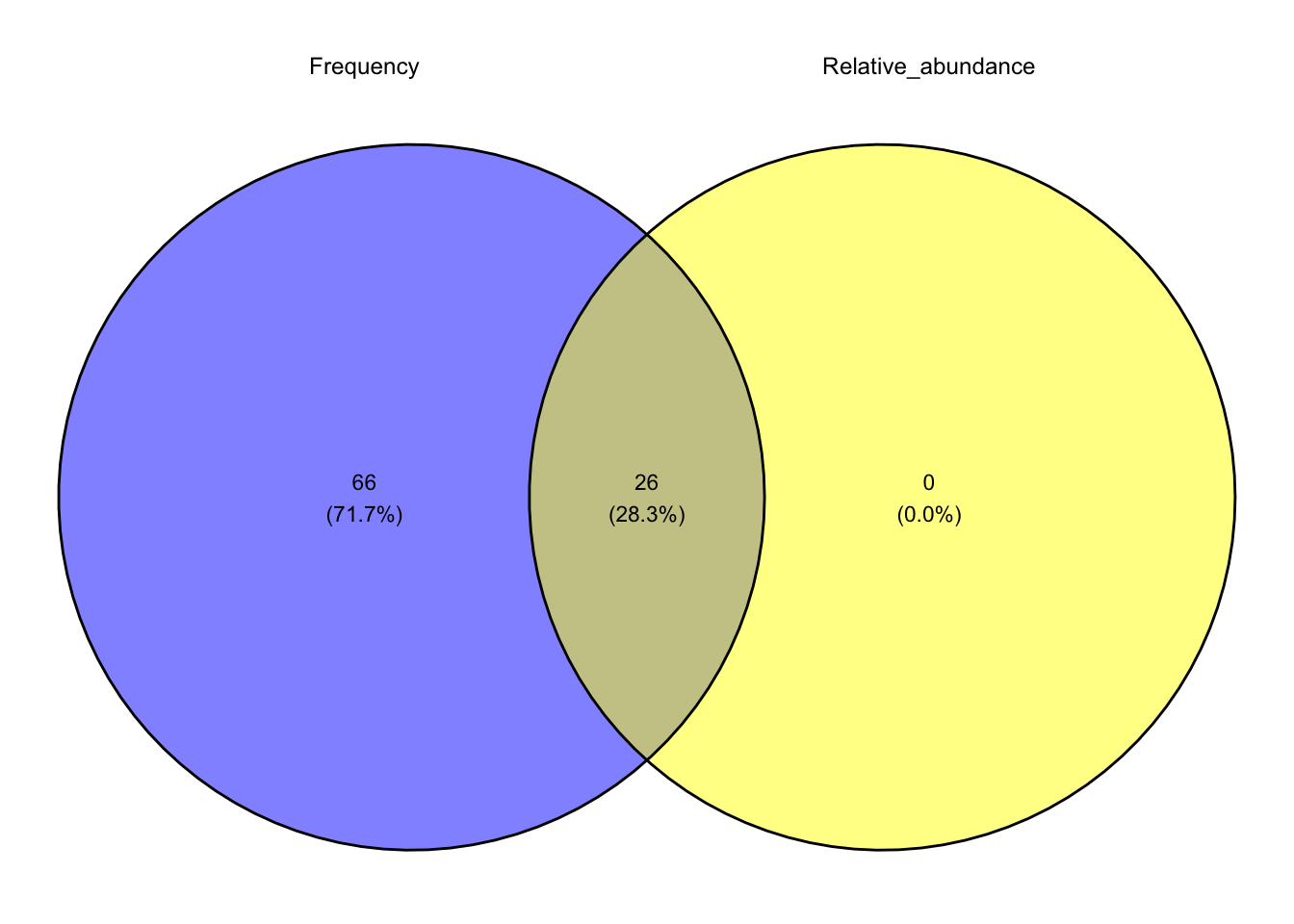

  1. Get the list of your core taxa based on the 95th percentile.
Core.95.intersect <- Reduce(intersect, Core.95.list)
  1. Subset your original phyloseq object for core taxa.
ps.Core <- subset_taxa(ps.dataset, Genus %in% c(Core.95.intersect))
  1. Fix the relative abundance of the core taxa to continue with the plot.
# Agglomerate taxa by genus level
Core_genera <- tax_glom(ps.Core, taxrank = "Genus", NArm = FALSE)

# Get relative abundance in %
Core_genera.RA <- transform_sample_counts(Core_genera , function(x) 100 * x/sum(x))

#Transform to a data frame
df.Core_genera <- psmelt(Core_genera.RA)
  1. Create a bubble plot. You can customize your plot using ggplot2 package available options.
df.Core_genera %>%
  group_by(Genus, Rotation, Location,) %>%
  summarize(abundance = mean(Abundance)) %>%
  ggplot(aes(Rotation, Genus)) +
  facet_wrap(~Location) +
  geom_point(aes(size = abundance), color = "grey30", fill = "#66A61E",
             alpha = 0.5, shape = 21, stroke = 0.1) +
  scale_size_continuous(range = c(0,8), breaks = c(1, 3, 5, 8, 10),
                        name="Relative\nAbundance (%)") +
  scale_x_discrete(name ="Rotation") +
  theme_bw()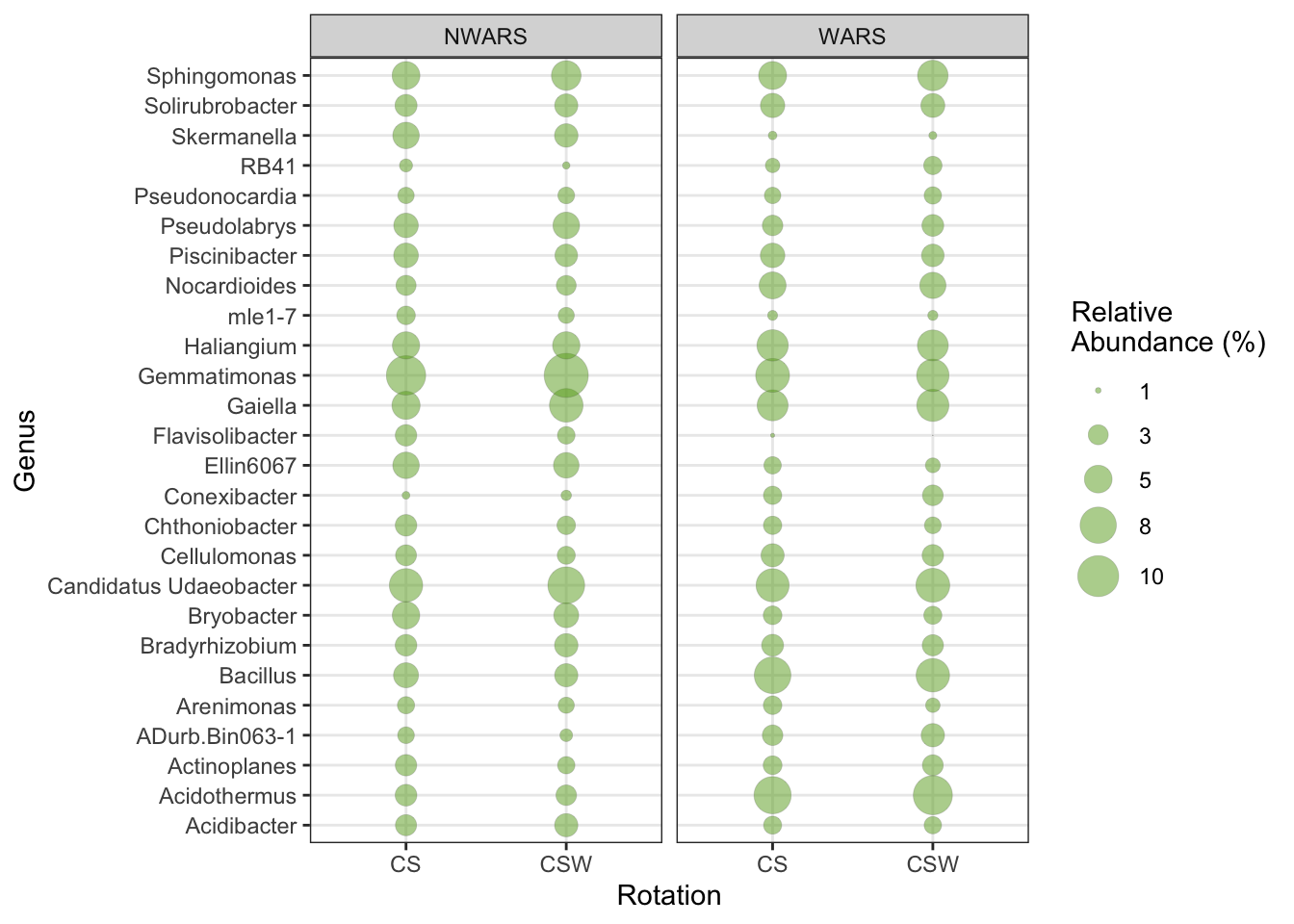

Back to top

Footnotes

  1. Shade et al. 2012 DOI:https://doi.org/10.1111/j.1462-2920.2011.02585.x↩︎

  2. (you can create that dir in the dialog box if needed↩︎

  3. Cantoran et al. 2023 DOI:https://doi.org/10.1093/femsec/fiad098↩︎